微分方程式による数理構造の解明をめざして

S 波入射とモードの変換

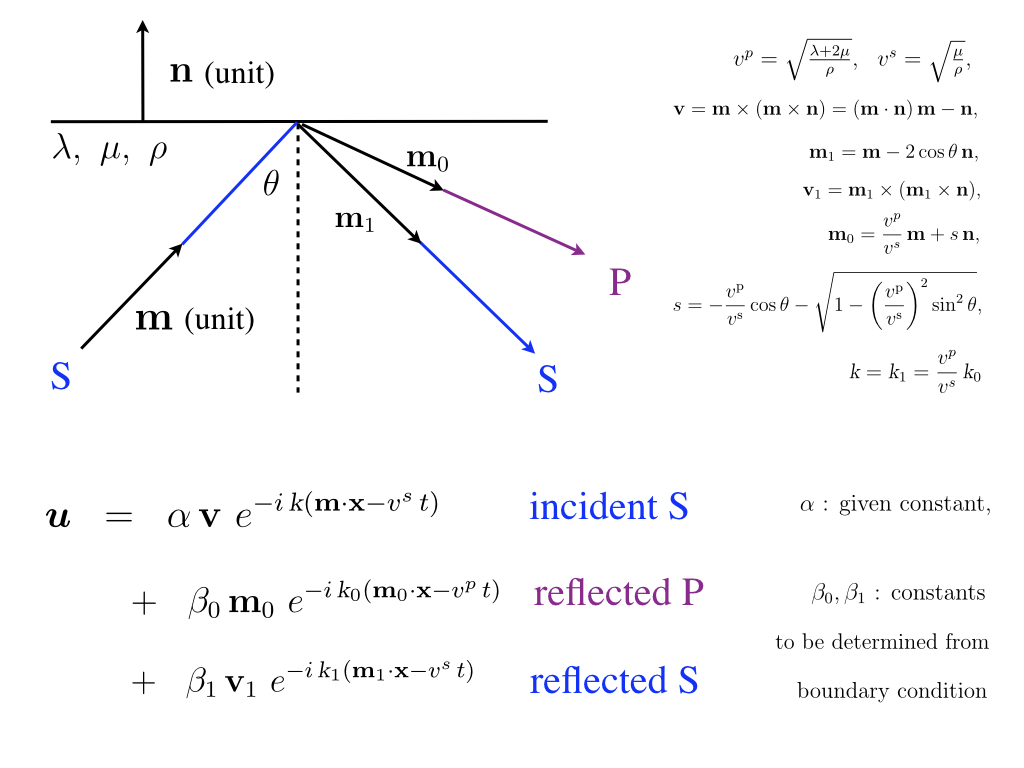
微分方程式とは未知関数とその導関数が満たす関係式のことです．その未知関数を微分方程式の解とよびます．物理，化学，生物学．工学，経済学等，様々な場面での現象が，微分方程式をもちいた数学モデルとして表現されます．そして微分方程式の解の性質を精査することで、現象に含まれる数理構造を解明していくことが研究の大きな動機であり，抽象的な理論が多い数学の中でもかなり現実的な，応用的色彩の強い分野といえます．現在私は，波動現象を記述する微分方程式の解をもとに，弾性波の性質を考察しています．地球を弾性体とみなすと，地震のときに震源から最初に到達する波がP波（縦波），つぎに遅れて到達する波がS波（横波）です．このP波，S波は反射の際，興味ある現象を起こします．S波を境界面に入射するとS波が反射されますが（スネルの法則．この法則も微分方程式の解を使って“証明”できます），反射波としてP波も発生します．これをモードの変換とよんでいます．図は，性質に偏りのない等方的弾性体におけるモードの変換を，微分方程式の一つである弾性波動方程式の解uを求めることで正当化したものです．一方，偏りをもった非等方弾性体に対して，弾性波動方程式の解から反射角や反射波の伝播速度を求めるなどの問題が、これからの研究テーマとなります．微分方程式を追うことで現象をより詳しく解明していくという，苦しいながらも有意義な研究をめざしています．

教授 田沼 一実 TANUMA kazumi
研究キーワード 微分方程式，弾性理論，非等方弾性体，弾性波，圧電体，表面波，逆問題
研究分野 解析学応用数学
主な研究テーマ
  • 非等方弾性体方程式の数学解析
  • 弾性波，弾性表面波の数理構造の研究
  • 圧電体方程式と圧電体表面波の研究
研究概要

微分方程式の数学研究。対象は，数理物理に現れる，弾性体や圧電体，導電体等を記述する微分方程式である。現象をモデル化することで得られた微分方程式に対して，その解の挙動を詳細に考察することで，現象を支配する原理を明らかにし，現象をより詳しく説明することで，現象にフィードバックする立場で研究を進めている。表面波速度の摂動公式・分散公式の導出，表面波データから非等方性や圧電係数，残留応力を同定する逆問題解析，インピーダンストモグラフィーの数理モデル化と再構成公式の導出，等の研究を行っている。
提供できる技術 ・応用分野

弾性体の数学理論，弾性波，弾性表面波，圧電体の表面波の数理的解析，impedance tomography 逆問題の数理
主要な所属学会

日本数学会，日本応用数理学会
論文
  • On the perturbation of Bleustein–Gulyaev waves in piezoelectric media. In: Itou, H., Hirano, S., Kimura, M., Kovtunenko, V.A., Khludnev, A.M. (eds.) Mathematical Analysis of Continuum Mechanics and Industrial Applications III, Proceedings of the International Conference CoMFoS18, Mathematics for Industry vol. 34, pp. 67-79. Springer (2020)
  • Monitoring near-surface depth profile of residual stress in weakly anisotropic media by Rayleigh-wave dispersion, Wave Motion, 77: 119-138, (2018)
  • Dispersion of Rayleigh waves in weakly anisotropic media with vertically-inhomogeneous initial stress, International Journal of Engineering Science, 92: 63-82, (2015)
最終更新日：