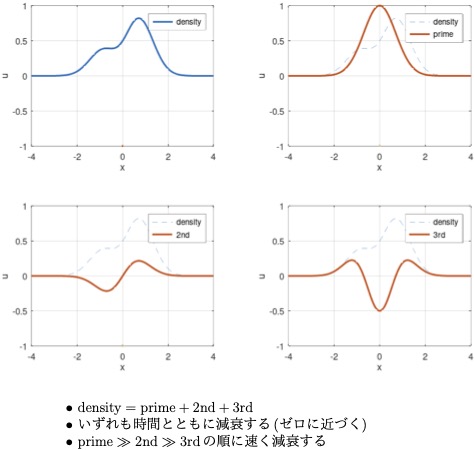
粒子の拡散現象

自然科学や社会科学、さらには身近に見られる「拡散現象」を数学的に捉える研究をしています。拡散現象の身近な例としては、例えばストーブやエアコンの暖気が部屋全体に拡がるのは熱の拡散ですし、加湿器を使って部屋の湿度を上げるのは水蒸気の拡散を利用しています。他にもお風呂にお湯を張るとき、蛇口から勢いよく出たお湯がすぐに静かな流れに落ち着くのも、流速がお湯の粘性によって拡散するからです。少し専門的なところでは、PCやスマホの内部で信号を伝える電荷は、熱力学的効果と電気的な相互作用によって半導体中に拡散します。これらはいずれも直接観測するのに困難を伴う現象です。本研究室では、それぞれの拡散現象を記述する拡散方程式の解を通して、現象の時間発展を捉える研究を行っています。

教授 山本 征法 YAMAMOTO masakazu
研究キーワード 半線形拡散方程式，非圧縮性粘性流体，走化性生物モデル，気象モデル，電界効果型トランジスタ
研究分野 解析学応用数学
主な研究テーマ
  • 非圧縮粘性流体の時間大域挙動に関する研究
  • 解の漸近展開に関する研究
  • 半線形拡散方程式の可解性の研究
研究概要

物理現象、生物現象、社会現象に現れる拡散について研究を行っています。取り扱う対象は、粒子の密度や質量、人口密度や生物の生息密度、温度やエネルギー、あるいは速度や運動量などで、これらの量はあらゆる場面で拡散したり集合したりします。特に興味深いのは、取り扱う量がそれ自身の影響を受ける非線形現象です。当研究室では、これらの量を解とする非線形拡散方程式の可解性、解の滑らかさの評価や時間大域挙動を研究しています。近年は特に、非圧縮性粘性流体の流速が時間とともにどのように変化するかに興味を持っています。流速とそれに伴って生ずる渦との間には、電磁気学におけるビオ・サバール則に相当する同値関係が知られていますが、数学的な背景により、流速よりも渦度の方が解析が容易です。現在これを利用して、流速の成分を時間大域的に主要なものから順に抽出する研究を行っています。
提供できる技術 ・応用分野

拡散現象の数学解析，現象の数理モデル構築
主要な所属学会

日本数学会
論文
  • Parabolic-scalings on large-time behavior of the incompressible Navier-Stokes flow, Nonlinear Anal. Real World Appl. 85 (2025), 104350. doi:10.1016/j.nonrwa.2025.104350
  • Time evolution of the Navier-Stokes flow in far-field, J. Math. Fluid Mech. 26 (2024), 67.doi:10.1007/s00021-024-00904-0
  • Optimal estimates for far field asymptotics of solutions to the quasi-geostrophic equation, Proc. Amer. Math. Soc.149 (2021), 1099-1110. doi:10.1090/proc/15305
最終更新日：